El Juicio
La lógica formal analiza el juicio en tanto en cuanto premisa del razonamiento, es decir, en relación tan sólo con la doctrina de la estructura de las demostraciones. El juicio es un proceso de aprehensión del objeto por el intelecto. Las diversas formas del juicio constituyen los eslabones, los elementos de este proceso. El juicio es un pensamiento en el que se afirma o se niega algo. Según Aristóteles, el juicio es el pensamiento compuesto de más de una idea, pero dotado a la vez de una unidad especial que se logra por medio de la cópula.
El juicio es la representación mental mediante la cual afirmamos o negamos el ser o la existencia de las cosas y es considerado un pensamiento central dentro del conocimiento. El juicio no sería posible si no existieran los conceptos y se lleva a cabo cuando la mente logra captar por simple aprehensión 2 conceptos y establecer una relación entre ellos mediante un nexo lógico verbal.
Así, en unos juicios se recoge el conocimiento verídico ya conseguido
acerca del objeto, y en otros, el probable; se supone tan sólo que el objeto
posee o no ciertos caracteres y rasgos; en los terceros, los interrogativos, se infiere la existencia de propiedades, caracteres o relaciones de algún objeto.
La vieja lógica delimita estrictamente estas diversas formas de juicios y no
consideraba la interrogación como un juicio.
Hoy día, la interpretación dada por Aristóteles a la esencia de los
juicios, pese a su sana base materialista, no puede satisfacernos, no resulta
suficiente. Aristóteles creó la doctrina de los juicios con vistas a su teoría
del razonamiento, mejor dicho, silogística, y por ello se limitaba a
pensamientos que pudieran servir de premisas para el razonamiento.
sin embargo, las diversas formas de juicios están recíprocamente
vinculadas. El juicio probable, que surge durante el desarrollo del
conocimiento, engloba los juicios verídicos que le han originado, y esto
significa que también en él hay elementos fidedignos. Por otra parte, todo
juicio verídico como pensamiento en desarrollo, contiene un cierto factor de
probabilidad de aproximación.
Los elementos del juicio son: sujeto, predicado y verbo:
- El sujeto es el objeto de juicio, es el concepto del cual se afirma o predica algo.
- El predicado es lo que afirma o niega acerca del sujeto, es lo que se predica del sujeto.
- El verbo es la parte esencial de un juicio, ya que no sólo une al sujeto con el predicado, sino que además expresa la relación necesaria con el ser. También se divide por su nexo.
El juicio: Concepto, estructura y características by Alejandra Márquez Dorantes (prezi.com)
Tradicionalmente los juicios se clasifican por su cantidad, cualidad y relación.
Por su cantidad son: universales, particulares y singulares.
Por su cualidad son: afirmativos, negativos y categóricos.
Por su relación; categóricos, hipotéticos y disyuntivos.
Por su modalidad: Problemáticos, asertóricos y apodícticos.
1.2 Las proposiciones categóricas, definición, estructura, las proposiciones categóricas de forma típica.
Las proposiciones categóricas son aquéllas que hacen afirmaciones incondicionales. Por ejemplo, todos los hombres son mortales es una proposición categórica, mientras que: si tengo el día libre, voy a la playa no lo es, ya que hay un condicionante para el hecho de ir a la playa: que tenga el día libre.
La forma general de toda proposición categórica es la siguiente:
cuantificador + sujeto + cópula + predicado
Donde: • El cuantificador determina si la proposición se refiere a todos los sujetos de un conjunto, a una parte de ellos o sólo a un elemento del conjunto.
• El sujeto es el conjunto o subconjunto de individuos o cosas de los que trata la proposición.
• La cópula (es decir, lazo) es el verbo que une al sujeto con el predicado. Tiene la doble función de llevar a cabo esta relación y de hacer posible el enunciado.
• El predicado es lo que se afirma o niega del sujeto.
Para fines de codificación de proposiciones categóricas, es decir, para su representación en lenguaje lógico, de lo que hablaremos con más detalle posteriormente, es muy recomendable obtener un predicado nominal equivalente para todos aquellos predicados mixtos o verbales. Por ejemplo:
•Las llamas convirtieron todo en cenizas. Se puede expresar como “todo fue convertido en cenizas por las llamas”.
•Juan estudia matemáticas.
Se puede expresar como “Juan es estudiante de matemáticas”.
Estas proposiciones están
clasificadas de acuerdo a su cantidad y calidad. En cuanto a su cantidad pueden
ser universales, particulares o singulares. En cuanto a su calidad pueden ser
afirmativas o negativas.
1.3
Calidad, Cantidad y Distribución:
Toda
proposición categórica de forma típica se dice que tiene una calidad y una
cantidad. La calidad de una proposición es afirmativa o negativa según que la
inclusión de clases sea afirmada o negada por la proposición. Así la universal
afirmativa y la particular afirmativa son ambas afirmativas en calidad,
mientras que la universal negativa y la particular negativa son ambas
negativas. Se acostumbra usar las letras A, E, I, O como nombres de las cuatro
formas típicas de proposiciones categóricas, la universal afirmativa, la
universal negativa, la particular afirmativa y la particular negativa,
respectivamente.
El uso de las letras como nombre proviene, según la cantidad
de una proposición y si es universal o particular según que la proposición se
refiere a todos o solamente a algunos de los miembros de la clase
designada por el término sujeto.
Así las proposiciones A y E son universales en cantidad, mientras que las proposiciones 1 y O son particulares, Observemos que los nombres universal y afirmativa, universal negativa, particular afirmativa y particular negativa describen inequívocamente las cuatro formas típicas mencionando primero su cantidad y luego su calidad.
Toda proposición categórica de forma típica comienza con una de las palabras todos, ningún y algunos. Estas palabras indican la cantidad de la proposición y son llamadas cuantificadores. Los dos primeros indican que la proposición es universal, el tercero que es particular, Además de expresar la cantidad universal, el cuantificador sirve para indicar la calidad negativa de la proposición E.
Algunos emperadores romanos eran
monstruos. Todos los comunistas son fanáticos.
Algunos soldados no serán héroes.
Los símbolos 'eran', 'son' y 'serán' sirven de cópula. El
esqueleto o esquema general de una proposición categórica de forma típica
consta de cuatro partes: primero, el cuantificador; luego, el término sujeto;
luego, la cópula, y, finalmente, el término predicado.
En
la interpretación basada en las clases, los términos sujeto y predicado de una
proposición categórica de forma típica designan clases de objetos y se considera
que la proposición misma se refiere a estas clases. Claro está que las
proposiciones pueden referirse a las clases de diferentes maneras. Puede
referirse a todos los miembros de una clase o solamente a algunos de ellos.
Así, la proposición:
Todos los diputados son
ciudadanos.
se refiere O trata de todos
los diputados, pero no de todos los ciudadanos. Afirma que cada miembro de la
clase de los diputados es un ciudadano, pero no afirma nada acerca de todos los
ciudadanos. No afirma que cada ciudadano sea un diputado.
pero tampoco lo niega. Se ve,
pues, que toda proposición A de esta forma: Todo S es P.
se refiere a todos los miembros de la clase designada por su término sujeto 'S', pero no se refiere a todos los miembros de la clase designada por su término predicado' P'.
Una proposición E se refiere a
todos los miembros de la clase designada por su término sujeto y, por lo tanto,
lo distribuye, por otra parte, al afirmar que la totalidad de la clase de los
atletas este excluida de la clase de los vegetarianos, afirma también que la
totalidad de la clase de los vegetarianos está excluido de la clase de los
atletas. La proposición dada afirma claramente de cada vegetariano que no es un
atleta. Una proposición E se refiere, por consiguiente, a todos los
lineamientos de la clase designada por el término predicado, en este caso,
decimos entonces que también distribuye su término predicado. Las proposiciones
E distribuyen tanto su término sujeto como su término predicado.
La referencia se dirige a la totalidad de esta clase, del mismo modo que, cuando se excluye a un hombre de un país, todas las partes de este país son inaccesibles para él. La proposición particular negativa distribuye su término predicado, pero no distribuye su término sujeto.
CALIDAD, CANTIDAD y DISTRIBUCION - LAS PROPOSICIONES CATEGORICAS (1library.co)
Afirmar que la clase designada por 'S' tiene miembros equivale a negar que sea vacía. Afirmar que hay S es negar la proposición simbolizada por 'S = 0'. Simbolizamos esta negación cruzando con una raya oblicua el signo de igualdad. La desigualdad 'S # 0' afirma que hay S mediante la negación de que S sea nula.
Las proposiciones categóricas típicas se refieren a dos clases y, por consiguiente, las ecuaciones que las representan son un poco más complicadas. Si cada una de las dos clases tiene ya un símbolo que las designa, la clase de todas las cosas que pertenecen a ambas puede representarse colocando uno junto al otro los símbolos de las dos clases originales.
Por ejemplo, si la letra' S' designa la clase de todas las sátiras y la letra ' P' la de todos los poemas, entonces la clase de todas las cosas que son al mismo tiempo sátiras y poemas se representa con el símbolo' SP', que designa la clase de todos los poemas satíricos. La parte común, o los miembros comunes. a las dos clases es llamado el 'producto' o la 'intersección' de las dos clases. El producto de dos clases es la clase de todas las cosas que pertenecen a ambas.
Podemos representar diagramaticamente las proposiciones mediante los diagramas de las clases a las cuajes se refieren. Representamos una clase por un círculo rotulado con el término que designa a esa clase. Así, la clase S es representada mediante un diagrama como el de la figura 3. Éste es el diagrama de una clase, no de una proposición. Simplemente, representa a la clase S, pero no hace ninguna afirmación acerca de ella. Para diagramar la proposición que afirme la ausencia de miembros no sea, que no hay ningún S, sombreamos todo el interior del círculo.
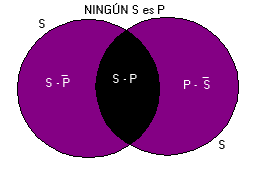
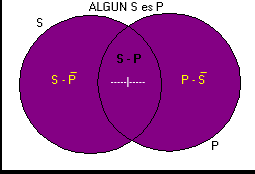
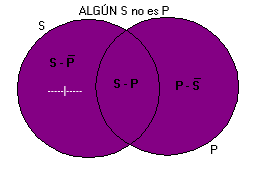
Los Diagramas de Venn constituyen una representación gráfica de las proposiciones categóricas de forma típica, en la cual las inclusiones y exclusiones espaciales corresponden a las inclusiones v exclusiones no espaciales de las clases. No solamente provienen de un método excepcionalmente claro de notación, sino que constituyen también la base de los métodos más simples y directos para determinar la validez de los silogismos categóricos.
Proposiciones Categóricas y Diagramas de Venn (paginasobrefilosofia.com)
Universal afirmativa: En este Esquema se nos ofrece una doble información acerca del por que Todos los S son P.
1.5 Traducción de proposiciones atípicas a forma típica:


.png)